1. Name of Experiment:
    ------------------
    Measurement of Photon Leakage Spectra from Spherical and Hemispherical Samples
    of Aluminium, Titanium, Iron, Copper, Zirconium, Lead, and Uranium-238 with a
    Central 14-MeV Neutron Source (1992).

 2. Objective of Experiment:
    -----------------------
    Measurement of spectra and leakages of photons from thick spherical and hemispherical
    samples of the most commonly used structural materials irradiated with a Central
    14-MeV Neutron Source for validation of existing nuclear data on gamma-production
    of these elements.
      
 3. Description of Source and Experimental Setup:
    --------------------------------------------
    The experimental configuration is presented in Fig. 1.
    An installation NG-200 (200-KeV deuteron accelerator with the current of separated
    D+ ion beam of up to 1 mA) was used as 14-MeV neutron source. The target was a
    zirconium foil saturated with tritium. Design of the target unit is presented in
    Fig. 2. The target was placed in the centre of spherical samples of inside diameter
    Øin=100 mm and outside diameter Øout = 200 mm. Weights of the samples used are
    given in Table 1.
      
 4. Measurement System and Uncertainties:
    ------------------------------------
    The measurements were performed using a scintillation detector having a stilbene
    crystal with dimensions of Ø 60 x 60 mm. Gamma-neutron separation was done using
    the scintillation pulse shape. 
    Direct 14-MeV neutrons from the target that were not scattered by the sample were
    delayed by a steel rod of diameter Ø 30 mm and length L=400 mm, placed in the
    immediate vicinity of the sample.
    Between the source and the detector, a concrete 1.5-m thick wall with a collimator
    was situated (Fig. 1). To reduce the background of scattered photons and cosmic
    rays the detector was placed in a shield of 50-mm thick lead bricks. In addition,
    to reduce the background from secondary gamma-rays falling on the detector due to
    interaction of neutrons with materials surrounding the detector, a polyethylene
    cylinder of diameter 100 mm and length L=200 mm was placed into the collimator.
    The cylinder substantially (approximately by 10 times) absorbed neutrons and not
    very heavily (2-3 times) absorbed gamma-rays.
    The 14-MeV neutron flux was measured with an all-wave detector pre-calibrated in
    absolute measurements of the neutron flux of the installation. These absolute
    measurements were conducted using the activation method and the reaction
    Al-27(n,alpha)Na-24. When replacing the samples, the indications of the all-wave
    detector were adjusted according to the flux amplification/attenuation coefficient
    of the samples used. The coefficients were measured experimentally as a
    relationship of count rate of the all-wave detector with and without the sample.
    These coefficients are presented in Table 2.
      
4.1. Measuring equipment and processing of experimental spectra.
     The photon spectra were measured using a scintillation detector having a stilbene
     crystal with dimensions of Ø 60x60 mm. Measured energy range is 0.3-8.0 MeV.
     Energy distribution for lines Co-60 (1.17 and 1.33 MeV) was about 10%. At energies
     higher than 3 MeV it was enhanced up to 6-7% and at energies lower than 0.5 MeV
     it went down to 15-20%.
     The choice of the stilbene crystal makes it possible to avoid many difficulties,
     namely: It is easy to solve the problem of neutron-gamma separation using
     scintillation pulse shape.
     Neutron activation of the detector material doesn’t disturb results.
     Practically the only type of photon interaction with the crystal material is the
     Compton effect which makes the mathematical processing of the primary
     experimental spectra significantly easer.
     Comparatively poor energy resolution of this method is of little importance for
     the problem of verification of gamma-production data used in various practical
     calculations. Processing of experimental electron-recoil spectra for transferring
     them into the photon spectra, was conducted using the method of “generalized
     differentiation”. The method is described in detail in paper [1].
     The results of measurements are presented in Table 3.

4.2. Measurement uncertainty.
     The measurement uncertainty is a sum of the following components: 
      
     Statistical uncertainty 
     This uncertainty is rather great mainly due to the principle of obtaining of
     results by the differentiation method. Although the total amount of counted
     pulses in each spectrum reaches (1.5-2)·106, the calculation of the effect as
     a difference of great numbers in narrow energy ranges leads to a noticeable
     statistical uncertainty especially at low energies. The value of this uncertainty
     depends greatly on the form of investigated spectra of each specific sample.
     The uncertainty of the main lines is estimated within the limits of ∆1=+-5 % for
     all elements. This uncertainty can be inferred for example from the photon
     spectra of spheres and hemispheres of one element. We can see the repeat of the
     spectra structure typical for the given element against the background of
     uncorrelated fluctuations conditioned by statistical uncertainty.
      
     Uncertainty in the detector efficiency.
     The detector efficiency was determined by measuring the spectra of (reference)
     standard preparations of 22Na, 137Cs, 60Co, 24Na. Within the energy range
     0.5-3.0 MeV this uncertainty is estimated as +-5% and its value is primarily
     connected with the uncertainty in recalculation of gamma-fluxes of the standard
     preparations to the actual experimental configuration, which differ drastically.
     The standard preparations were placed at 25-50 cm from the detector, whereas in
     the real experiment the gamma-radiation came from the sample at a distance of
     8.5 m from the detector in the presence of the collimator, air and various
     objects in the experimental hall. Within the energy range 3-8 MeV the efficiency
     uncertainty may reach ∆2=7-8% due to the absence of standard preparations with
     such energy. Here we were used only calculations of intensities of the
     well-studied gamma-lines: 4.43 MeV for carbon and 6.13 MeV for oxygen.
  
     Uncertainty in mathematical processing of the experimental spectra.
     Origination of this uncertainty is connected with the uncertainty of knowledge
     of the response function for the detector throughout the range of measured
     photon energies. Fig. 3 and Fig. 4 show that after mathematical processing of
     the apparatus spectra of standard preparations, the photon spectra obtained
     still have oscillating “tails” of small minima and peaks. The height of these
     peaks does not exceed +-10% and on average makes up ∆3=+-7%, which indicates the
     obtained accuracy of processing.

     Summing all the above mentioned uncertainties, one can obtain for absolute values:

     

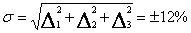     For the relative measurements and comparison of spectrum forms of various
     elements or samples, the accuracy is naturally better and reaches +- 5%.
      
 5. Description of Results and Analysis; Comparison with Calculations. 
    ------------------------------------
    Figures 5-11 show that the photon spectra are very various and individual for
    each element. The spectra of the hemispheres repeat the structure of the sphere’s
    spectra to small fluctuations in the order of +-5% of the intensities of the main
    peaks. This shows the high relative accuracy of the measurements performed. In
    some cases the spectra calculated using the code MCNP code with libraries ENDF/B6
    and ENDL-92 differ greatly from the experimental ones and fall far outside the
    limits of experimental uncertainty (See Zirconium, for example).

    Let us consider separately the situation for every element under study.
      
  - Aluminium. Fig. 5 and Fig. 6 show, that general form of the spectrum is repeated
    both in the calculations and in the experiments. However the intensities of
    these lines in different calculations and the experiment are different. Thus,
    for example, the very intensive in calculations line at 1.014 MeV does not
    confirmed by the experiment wherein it is at least 3 times lower. The total
    amount of photons in the experimental spectra is close to the ENDF-B/5
    calculations.
    It should be noted that 14-MeV neutrons cause reaction Al-27(n,alpha)Na-24. The
    generated 24Na decomposes (half-life is about 15 hours), emitting gamma-quanta
    with energies of 1.37 and 2.75 MeV. In the process of measurements, these
    gamma-quanta belong to the spectrum measured. As a result, the form of the
    obtained spectrum depends on the time of measurements. If the process of
    measurements takes less than the half-life period (as in our case we have), the
    contribution of these lines occurs to be minor, and in long-term many-hour
    measurements an equilibrium distribution is established, wherein the intensity
    of these lines rises sharply.
  - Titanium (see Fig. 7 and Fig. 8).
    For titanium very significant discrepancies are observed between the
    calculations and the experiments. In the calculated spectra only one 0.511 MeV
    line of positron annihilation is seen. The presence of this line in all the
    samples is due to the effect of positron annihilation. The rest part of the
    calculated spectra is presented by continuous distribution, while the experiment
    gives complex spectra form with the lines at 0.889, 0.983, 1.438, and 2.315 MeV.
    These lines are well-known from the Atlas [2]. The total amount of photons in
    the ENDF/B-6 calculation is nearly two times greater than that in the experiment.
  - Iron (see Fig. 9 and Fig. 10).
    Iron is the most studied element. However, there are also discrepancies
    for iron but they are not such large as for other elements. The total amount of
    photons in the calculations and experiments differ insignificantly (within 10%).
  - Copper (Fig. 11).
    Our experimental data for copper are significantly differ from the
    calculated ones. It seems that there are no reliable experimental data for
    this element at all.
  - Zirconium (Fig. 12 and Fig. 13).
    Unfortunately, the ENDF/B6 version available for us has no data on the gamma-
    production for zirconium. Besides the base 2.188 MeV line and the 0.511 MeV
    line common to all elements, the zirconium experimental spectra have one twin
    line at 0.912 and 0.935 MeV, not separating in our experiments. In the ENDL-92
    calculation these lines are not present. At the same time the continuous component
    of spectrum in the calculation is much overestimated. The total amount of photons
    in the calculation with ENDL-92 is 24% higher than that in the experiment.
    The total photons energy in the experiments and calculations agree nearly due
    to the difference in the spectra from.
  - Lead (Fig. 14 and Fig. 15).
    The experimental photon spectrum from lead agrees well with the ENDF/B6
    calculations throughout the whole energy range. The calculation ignores the
    experimental line close to 2.2 MeV.
  - Uranium-238 (Fig. 16 and Fig. 17).
    The calculated gamma-spectrum of uranium is distinct not very significantly
    from the experimental one. In the experiment, a certain structure is
    outlined in the form of lines at 0.5, 1.2, 2.3, and 4.4 MeV. The last two
    peaks are probably connected with the experimental configuration and the
    scattered background (capture of slow neutrons by hydrogen of concrete walls
    and inelastic scattering 14-MeV neutrons in polyethylene).

    Summarizing the analysis of the results, it is possible to say that there is
    significant difference in gamma-production of the calculations and the
    experiments even for the most common elements, and the accepted systems of
    nuclear data should be appropriately updated. Besides, it should be noted
    that the studies conducted refer only to the energy region of incident
    neutrons close to 14 MeV. The region of intermediate neutron energies 5-14 MeV
    is still unstudied, and it is possible to suppose that the discrepancies
    between the calculations and experiments in this range will be even greater.

    The problem of correlation between total neutron cross-section and
    gamma-production cross-section still remains unclear. If such correlation
    exists, the functions of photon leakage depending on the neutron energy
    may be very complicated (according to the structure of full cross-sections).
    Therefore, the extrapolation of data on photon-production into unstudied
    region of neutron energies will be unreliable. It is necessary to conduct
    experiments on gamma-leakage for neutron energies ranging from 5 to 10 MeV.
      
 6. Special Features of the Experiment:
    ----------------------------------
    Method of generalized differentiation with semi-empirically determined
    coefficients for transferring apparatus electron-recoil spectra into
    energy spectra.

 7. Author/Organizer
    ----------------
    Experiment and analysis:
    A.I. Saukov, V.D. Lyutov, E.N. Lipilina
    RFNC-VNIITF
    (Zababakhin Russian Federal Nuclear Center – 
    All-Russian Scientific Researching Institute of Technical Physics)
    Vasiliev Street 13, P.O. Box 245
    Snezhinsk
    Chelyabinsk Region
    456770 Russia

    Compiler of data for SINBAD:
    Elena N.Lipilina
    RFNC-VNIITF

    Reviewer of compiled data:
    I. Kodeli
    OECD/NEA, 12 bd des Iles, 92130 Issy les Moulineaux, France

 8. Availability:
    ------------

    Unrestricted

 9. References:
    ----------

    [1] A.I. Saukov, B.I. Sukhanov, V.D. Lyutov, et al, "Proton Leakage from Spherical
        and Hemispherical Samples with a Central 14MeV Neutron Source", Nucl.Sci.Eng.,
        V.142, No.2, p.158, 2002
    [2] M.R. Ahmed, A.M. Demidov, et al, "Atlas of gamma-ray spectra from the inelastic
        scattering of reactor fast neutrons", Moscow, Atomizdat, 1978
    [3] A. I. Saukov, E. N. Lipilina, V. D. Lyutov , "Measurements of Neutron and 
        Photon Leakage from Spherical and Hemispherical Samples with a Central 14-MeV
        Neutron Source as a Possible Type of Benchmarks", presented at the Int. Conf.
        on Radiation Safety, ICRS10 – RPS-2004, May 9-14, 2004, Madeira, Portugal

10. Data and format:

10. Data and format:
    Description of detailed files

No. Filename    Size(byte)  Contents
---------------------------------------------------------
 1  rfnc_ph.htm    19630  This information file	
 2  MCNP5.inp       1696  Input data for the MCNP5 calculation	
 3  fig1exp.jpg    40098  Fig. 1. Geometry of experiment	
 4  fig2mishen.jpg 48960  Fig. 2. Design of the target unit	
 5  fig3na22.jpg   25895  Fig. 3. Gamma-spectrum of Na-22 specimen	
 6  fig4na24.jpg   23682  Fig. 4. Gamma-spectrum of Na -24 specimen	
 7  fig5alsp.jpg   45547  Fig. 5. Calculated and experimental spectra
                          of photon yield from Al sphere 	
 8  fig6alhs.jpg   46422  Fig. 6. Calculated and experimental spectra
                          of photon yield from Al hemisphere 	
 9  fig7tisp.jpg   47585  Fig. 7. Calculated and experimental spectra
                          of photon yield from Ti sphere 	
10  fig8tihs.jpg   45727  Fig. 8. Calculated and experimental spectra
                          of photon yield from Ti hemisphere 	
11  fig9fesp.jpg   45593  Fig. 9. Calculated and experimental spectra
                          of photon yield from Fe sphere 	
12  fig10fehs.jpg  47799  Fig. 10. Calculated and experimental spectra
                          of photon yield from Fe hemisphere 	
13  fig11cusp.jpg  47492  Fig. 11. Calculated and experimental spectra
                          of photon yield from Cu sphere 	
14  fig12zrsp.jpg  43297  Fig. 12. Calculated and experimental spectra
                          of photon yield from Zr sphere 	
15  fig13zrhs.jpg  43534  Fig. 13. Calculated and experimental spectra
                          of photon yield from Zr hemisphere 	
16  fig14pbsp.jpg  47513  Fig. 14. Calculated and experimental spectra
                          of photon yield from Pb sphere 	
17  fig15pbhs.jpg  50146  Fig. 15. Calculated and experimental spectra
                          of photon yield from Pb hemisphere 	
18  fig16u8sp.jpg  43560  Fig. 16. Calculated and experimental spectra
                          of photon yield from U-238 sphere 	
19  fig17u8hs.jpg  49637  Fig. 17. Calculated and experimental spectra
                          of photon yield from U-238 hemisphere 	
20  tab1samples.txt  163  Table 1. Parameters of samples used	
21  tab2leakage.txt  192  Table 2. Total neutron yield from used samples
                          per one neutron of a 14 MeV source	
22  tab3result.txt 12488  Table 3. Results of measurements	
23  tab3result.xls 31744  Table 3. Results of measurements	
24  mad_rep.pdf   260641  Reference 3


SINBAD Benchmark Generation Date: 09/2005
SINBAD Benchmark Last Update: 03/2006